Quardratische Gleichungen
aus www.arndt-bruenner.de
Quadratische Gleichungen und Normalform
Wenn in einer ganzrationalen Gleichung (ohne x im Nenner, irgendwelchen Wurzeln oder sonstigen Funktionen) die Unbekannte mit der Hochzahl (=Exponent) 2 auftritt, also z.B. als x², und dieses x² auch nicht durch Umformungen wegfällt, spricht man von einer quadratischen Gleichung.
Solche Gleichungen kann man immer so umformen, zusammenfassen und umsortieren, daß "alles" auf einer Seite steht (auf der anderen Seite steht dann 0) und aus maximal drei Summanden besteht. Ein Summand enthält x² mit einem Faktor, einer x mit Faktor, und der andere ist eine Zahl ohne x.
Beispiel:
10x - 4(-3x + 1) - 2(x + 23)(x + 1) = -6 | Ausmultiplizieren der Klammern 10x + 12x - 4 - 2(x² + x + 23x + 23) = -6 | 10x + 12x - 4 - 2x² - 2x - 46x - 46 = -6 | Zusammenfassen gleichartiger Glieder -26x - 50 - 2x² = -6 | + 6 (alles auf eine Seite bringen) -26x - 44 - 2x² = 0 | Umsortieren, Reihenfolge: x², x, Zahl -2x² - 26x - 44 = 0
Nun kann man die Gleichung noch durch den Faktor vor dem x² teilen und bekommt so die Normalform der Gleichung:
-2x² - 26x - 44 = 0 |-2) (negative Divisoren müssen eingeklammert werden) x² + 13x + 22 = 0
Die Normalform quadratischer Gleichungen besteht immer zunächst aus dem x²;
dann aus einem x mit einem Faktor, den man mit p bezeichnet;
und zuletzt aus einer Zahl, die man mit q bezeichnet.
Die Summe dieser maximal drei Glieder ergibt 0. (Daher heißen die Lösungen auch Nullstellen.)
Die Zahlen p und q nennt man auch Koeffizienten einer quadratischen Gleichung. Im Beispiel oben sind die Koeffizienten p=13 und q=22.
Normalform der quadratischen Gleichung:
x² + px + q = 0
Falls kein x auftritt, so ist p=0, falls keine einzelne Zahl auftritt, ist q=0. Wenn in der Gleichung das x keinen Faktor besitzt, so ist p=1 oder p=-1, je nach dem Rechenzeichen vor dem x.
Lösungsweg
Wenn man sich den Term x² + 13x + 22 aus dem Beispiel oben anschaut, so kommt man vielleicht auf die Idee, daß das irgendwie das Resultat der Anwendung der ersten binomischen Formel sein könnte, was in etwa so aussehen müßte:
Zur Erinnerung: Das Modell der 1. binomischen Formel besagt, daß in der Mitte des Terms ohne Klammern das doppelte Produkt aus dem ersten und dem zweiten Summanden in der Klammer steht, also
Bei uns heißt dieser Summand 13x. Unser x ist das A. Das "?" steht an der Stelle von B. Wir müssen also herausfinden, was sich bei
Es ist natürlich 6,5.
Diese Zahl muß stets die Hälfte des Faktors vor dem x sein, also die Hälfte von p. Auch hier ist 13/2 = 6,5.
Mal sehen, was sich mit der 6,5 als zweitem Summanden im Binom ergibt:
(x + 6,5)² = x² + 13x + 42,25.
Schade, statt der 22 erhalten wir 42,25.
Um weiterzukommen und die Idee mit der binomischen Formel zur Lösung der Gleichung verwenden zu können, braucht man folgende zwei weitere Ideen:
- Wenn man weiß, welchen Zahlenwert ein Ausdruck wie (x + 6,5)² hat, kann man über die
Quadratwurzel(n) dieser Zahl berechnen, welche Wertex + 6,5 hat. Da da plötzlich kein x² mehr enthalten ist, kann man x leicht berechnen! Es wäre also ziemlich gut, wenn wir den Ausdruck auf der linken Seite der Gleichung als Binom(x + ?)² schreiben könnten! - Man kann die Gleichung doch ganz leicht so verändern, daß das klappt! Wir brauchen statt der 22 die 42,25, die das Quadrat der 6,5 in der Klammer ist, also müssen wir doch nur die Differenz zur Gleichung addieren!
Also, tun wir das einfach:
x² + 13x + 22 = 0 | + 20,25 x² + 13x + 42,25 = 20,25
Nun kann man die linke Seite als Binom schreiben:
(x + 6,5)² = 20,25
Beim Ziehen der Quadratwurzel auf beiden Seiten der Gleichung muß man beachten, daß immer zwei verschiedene Zahlen mit sich selbst malgenommen ein bestimmtes Produkt ergeben, nämlich die "normale" Quadratwurzel und ihre negative Gegenzahl. Es ist 2·2=4, aber auch (-2)·(-2)=4.
Das wird beachtet, indem man beim Ziehen der Wurzel aus beispielsweise 4 die beiden Fälle
Wenn auf beiden Seiten der Gleichung die positive und die negative Quadratwurzeln gezogen werden sollen, gibt es somit eigentlich vier Fälle:
Fall 1 und Fall 4 sind äquivalent, denn sie gehen durch Multiplikation mit
Man muß also ab hier zwei Fälle unterscheiden, die mit dem logischen Ausdruck "oder", lateinisch vel, getrennt werden, abgekürzt mit dem kleinen v, abgeleitet von "vel":
(x + 6,5)² = 20,25 | ± √ x + 6,5 = 4,5 v x + 6,5 = -4,5 | - 6,5 x = -2 v x = -11
Damit ist die Lösungsmenge L={-11; -2}. Nacheinander Einsetzen der Lösungen in die ursprüngliche Gleichung ("Probe") bestätigt die Lösungen.
Allgemein muß man also ausgehend von der Normalform die Gleichung so verändern, daß die einzelne Zahl das passende zweite Quadrat des Binoms darstellt.
Dies nennt man quadratische Ergänzung.
Diese zweite Zahl des Binoms ist, wie wir oben herausgefunden haben, die Hälfte von p.
Damit muß die einzelne Zahl in der Gleichung (p/2)² sein.
Man ergänzt die Gleichung x² + px + q = 0 so, daß auf der linken Seite anstelle von q die Zahl (p/2)² auftritt!
Beispiele für quadratische Ergänzung
x² + 4x - 5 = 0 p = 4 (p/2)² = 2² = 4
x² + 4x + 4 = 9 quadratische Ergänzung
(x + 2)² = 9
Fortsetzung: unten
x² - 7x + 10 = 0 p = -7 (p/2)² = (-3,5)² = +12,25
x² - 7x + 12,25 = 2,25
(x - 3,5)² = 2,25
x² - 3x - 28 = 0 p = -3 (p/2)² = 2,25
x² - 3x + 2,25 = 30,25
(x - 1,5)² = 30,25
Merke: Das Vorzeichen des zu ergänzenden Summanden ist immer positiv, da es ein Quadrat ist!
So geht's nach der quadratischen Ergänzung weiter:
(x + 2)² = 9 | Wurzel ziehen, unterscheide zwei Fälle (siehe oben)
x + 2 = -3 oder x + 2 = 3 | -2
x = -5 oder x = 1
L={-5; 1}
(x - 3,5)² = 2,25 | Wurzel ziehen
x - 3,5 = -1,5 oder x - 3,5 = 1,5 | + 3,5
x = 2 oder x = 5
L={2; 5}
(x - 1,5)² = 30,25 | Wurzel ziehen
x - 1,5 = -5,5 oder x - 1,5 = 5,5 | + 1,5
x = -4 oder x = 7
L={-4; 7}
Weitere Beispiele kann man sich →hier erzeugen lassen.
→ interaktive Beispiele zur quadratischen Ergänzung
→ große Übungsseite zum Umformen und Lösen von quadratischen und linearen Gleichungen
Lösungsformeln für quadratische Gleichungen
Wenn man die quadratische Ergänzung auf die Normalform mit den Koeffizienten p und q anwendet, erhält man eine Formel für die Lösungen.
x² + px + q = 0 | - q (Der Übersicht zuliebe weg mit der Zahl) x² + px = -q | + (p/2)² (quadratische Ergänzung) x² + px + (p/2)² = (p/2)² - q | als Binom schreiben (x + p/2)² = (p/2)² - q | positive und negative Wurzeln ziehen x + p/2 = ±√((p/2)² - q) | - p/2 x1/2 = -p/2 ± √((p/2)² - q)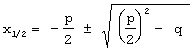
Man erhält die Lösungen der quadratischen Gleichung, indem man p und q abliest (p als Faktor vor dem x und q als die einzelne Zahl), in diese Formel einsetzt und den Term berechnet. Beachte dabei, daß das Quadrat der Klammer unter der Wurzel nichts anderes als das (immer positive) Quadrat der einfach zu berechnenden Zahl vor der Wurzel (-p/2) ist.
Die negative Wurzel ergibt die kleinere Lösung und die positive Wurzel die größere.
→ Übungen zum Lösen quadratischer Gleichungen mithilfe der p-q-Formel
Falls die quadratische Gleichung auch einen Faktor (≠1) vor dem x² enthält, dann nennt man die Koeffizienten a, b und c und schreibt die Gleichung allgemein
Die Lösungsformel ergibt sich dann so:
ax² + bx + c = 0 | : a
x² + b/a·x + c/a = 0 | - c/a
x² + b/a·x = -c/a | + (b/(2a))² (quadratische Ergänzung)
x² + b/a·x + (b/(2a))² = (b/(2a))² - c/a | als Binom schreiben
(x + b/(2a))² = (b/(2a))² - c/a | positive und negative Wurzeln ziehen
x + b/(2a) = ± √((b/(2a))² - c/a) | - b/(2a)
x1/2 = -b/(2a) ± √((b/(2a))² - c/a)
= -b/(2a) ± √(b² - 4ac)/(2a)
= (-b ± √(b² - 4ac))/(2a)
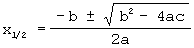
Diese Formel wird abc-Formel oder auch "Mitternachtsformel" genannt. Warum nur???? Hat sie etwa ein Herr Mitternacht um Mitternacht entdeckt??? Soll man sie nur zur Geisterstunde anwenden??? Soll man sie so in- und auswendig können, daß man sie sofort aufsagen kann, wenn man um Mitternacht geweckt wird — falls man da überhaupt schon schläft??? (Wer es besser weiß, der schickt mir bitte eine eMail!)
Weitere Erklärungen:
• Der doppelte Index bei x1,2 sieht aus wie 12(-Uhr-Mitternacht).
Existenz reeller Lösungen
In den Formeln und auch im manuellen Verfahren nach der quadratischen Ergänzung tauchen jeweils Quadratwurzeln auf. Bekanntlicherweise gibt es keine reelle Zahl, deren Quadrat negativ ist, denn jede Zahl ergibt mit sich selbst malgenommen eine positve Zahl. ("Minus mal minus ergibt plus.")
Falls der Wert unter der Wurzel (Radikand) negativ ist, kann man die Wurzel nicht ziehen, und es gibt folglich keine reelle Lösung der quadratischen Gleichung! (Es gibt jedoch immer zwei komplexe Lösungen: siehe diese Seite.)
Falls der Radikand 0 ist, ist die Wurzel 0, und es gibt nur eine Lösung, denn ±0 bleibt ja immer 0, d.h. der Term ist in beiden Fällen gleichwertig.
| Anzahl reeller Lösungen |
Form der Gleichung | Bedingung |
|---|---|---|
| 2 | p-q-Form | (p/2)² - q > 0 ⇔ p² > 4q |
| a-b-c-Form | b² - 4ac > 0 ⇔ b² > 4ac | |
| 1 | p-q-Form | (p/2)² - q = 0 ⇔ p² = 4q |
| a-b-c-Form | b² - 4ac = 0 ⇔ b² = 4ac | |
| 0 | p-q-Form | (p/2)² - q < 0 ⇔ p² < 4q |
| a-b-c-Form | b² - 4ac < 0 ⇔ b² < 4ac | |
Symmetrie und komplexe Nullstellen
Wie man an den Formeln sieht, sind die Lösungen stets symmetrisch zum (reellen) Wert -b/(2a) bzw. -p/2, denn der Wert der Wurzel wird entweder hierzu addiert oder hiervon subtrahiert. Wenn die Wurzel keine reelle Lösung haben sollte, also der Radikand D<0 ist, so ist der reelle Teil beider Lösungen der o.g. Wert -b/(2a) bzw. -p/2, und die imaginären Teile ergeben sich aus der positiven und der negativen Wurzel aus -D >0 mal die imaginäre Einheit î (die mit
x1/2 = -b/(2a) ± √(c/a - (b/(2a))²)·î



