Brüche addieren

aus www.frustfrei-lernen.de

Schritt 1: Brüche auf einen Nenner bringen

Um Brüche addieren zu können, müssen beide den selben Nenner haben. Zur Erinnerung: Der Nenner war das, was "unten" steht beim Bruch. Und der muss - wie eben schon angedeutet - für beide gleich sein. Wichtig dabei ist: Der Wert des Bruches darf sich nicht ändern. Dabei hilft folgendes Wissen: 1 von 2 gleich großen Stücken von einem Kuchen ist gleich viel wie 2 von 4 gleich großen Stücken eines Kuchens. Es folgt ein kleines Beispiel, anhand dessen zwei Möglichkeiten zur Lösung gezeigt werden.

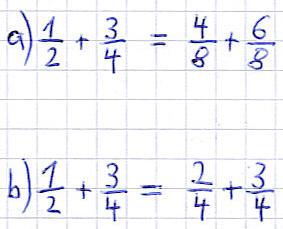
In beiden Fällen soll 1/2 + 3/4 auf einen Nenner gebracht werden. Dabei wurden die beiden eben genannten Möglichkeiten genutzt. Dies funktioniert wird folgt.

Variante a):

• Die beiden Nenner werden miteinander multipliziert. Da 2 · 4 bekanntlich 8 ist, ist der Nenner für die neuen Brüche 8.
• Der Zähler des ersten Bruches wird mit dem Nenner des zweiten Bruches multipliziert. Damit ergibt sich 1 · 4 = 4. Diese 4 ist der neue Zähler des ersten Bruches
• Der Zähler des zweiten Bruches wird mit dem Nenner des ersten Bruches multipliziert. 2 · 3 = 6. Diese 6 ist der neue Zähler des zweiten Bruches.

Tipp: Lest euch jeden Punkt der Variante a) noch einmal langsam durch und verfolgt diesen anhand des Beispieles a).

Variante b):

• Die 4 des zweiten Nenners ist ein Vielfaches der 2 des ersten Nenners. Um von 2 auf 4 zu kommen, wird mit 2 multipliziert. Also Zähler und Nenner mit 2 multiplizieren. Das Ergebnis ist oben zu sehen.

Welche Variante soll ich nutzen?

Die Variante b) ist meist kürzer. Wer sieht, dass die eine Zahl ein vielfaches der anderen ist, kann diese Variante nutzen. Wem das nicht gelingt, greift am Besten auf Variante a) zurück. Es gibt theoretisch noch eine weitere Möglichkeit unter Einsatz des größten gemeinsamen Teilers. Doch dies würde die Sache hier unnötig komplizieren. Wer sich unsicher ist: Variante a) funktioniert immer.

Schritt 2: Den Bruch addieren

Hat man den Bruch erst einmal auf einen Nenner gebracht, ist das addieren der Brüche ganz einfach. Die beiden folgenden Beispiele zeigen euch, wie dies funktioniert.

So funktioniert die Addition:

• Die beiden Zähler werden addiert und ergeben den Ergebniszähler
• Die Nenner sind überall gleich

Es ist also ganz simpel: Einfach die Zähler addieren und das wars. Der Nenner bleibt.

Schritt 3: Brüche kürzen

Habt Ihr Schritt 1 und Schritt 2 der Addition von Brüchen richtig durchgeführt, solltet ihr auf das richtige Ergebnis berechnet haben. Nun gibt es jedoch oft die Möglichkeit, dieses  noch zu vereinfachen. Es folgen erneut Beispiele.

Je kleiner die Zahlen sind, desto einfacher. Deshalb kürzt man die Brüche. Dies funktioniert, wenn Zähler und Nenner durch die gleiche Zahl ohne Rest teilbar sind.

• Beispiel links, oben: Zähler und Nenner des  Bruches lassen sich ohne Rest durch 3 teilen.
• Beispiel rechts, oben: Zähler und Nenner des Bruches lassen sich ohne Rest durch 2 teilen.
• Beispiel links, unten: Zähler und Nenner des Bruches lassen sich ohne Rest durch 2 teilen
• Beispiel rechts, unten: Hier kann nicht mehr gekürzt werden