Flächeninhalt

Flächenberechnung / Flächeninhalt/t-ocker.de
(nach und nach werden es mehr Formeln für die Flächenberechnung / den Flächeninhalt)

Flächen in der Ebene kann man aus bekannten Längenwerten und oder Winkeln berechnen. Nachfolgend Formeln zur Flächenberechnung.

Für alle Flächenformeln / zum berechnen von Flächen gilt:
A = Flächeninhalt
U = Umfang
D = Diagonalenlänge
a, b, c, d = Seitenlängen

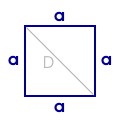
Quadrat:

1. alle Seiten sind gleich lang
2. alle Winkel sind rechte Winkel (90°)

Flächeninhalt: A = a²
oder A = a · a

Umfang: U = 4 · a

Diagonalenlänge: D = a · √2

weitere Formeln: Formel Quadrat

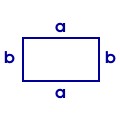
Rechteck:

1. gegenüberliegende Seiten verlaufen parallel
2. gegenüberliegende Seiten sind gleich lang
3. alle Winkel sind rechte Winkel (90°)
4. beide Diagonalen sind gleich lang

Flächeninhalt: A = a · b

Umfang: U = 2 · a + 2 · b
oder U = 2 · (a + b)

Diagonalenlänge: D = √a² + b²

weitere Formeln: Formel Rechteck

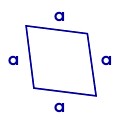
Rhombus / Raute:

1. alle vier Seiten sind gleich lang
2. gegenüberliegende Seiten verlaufen parallel
3. gegenüberliegende Winkel sind gleich groß
4. nebeneinander liegende Winkel ergeben 180°
5. Diagonalen stehen senkrecht aufeinander und halbieren einander
6. Innenwinkel werden durch die Diagonalen halbiert

(e und f sind die Diagonalen,
die Höhe h ist der Abstand zwischen den parallel verlaufenden Seiten)

Flächeninhalt: A = e · f : 2
oder A = a · h_aweitere Formeln: Formel Rhombus

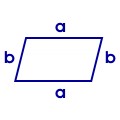
Parallelogramm:

1. gegenüberliegende Seiten verlaufen parallel
2. gegenüberliegende Seiten sind gleich lang
3. gegenüberliegende Winkel sind gleich groß
4. nebeneinander liegende Winkel ergeben 180°
5. jede Diagonale teilt es in zwei kongruente Dreiecke

(h_a und h_b - sind die Höhen im Winkel von 90° über a und b)

Flächeninhalt: A = a · h_a
oder A = b · h_bUmfang: U = 2 · a + 2 · b
oder U = 2 · (a + b)

weitere Formeln: Formel Parallelogramm

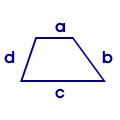
Trapez:

1. mindestens zwei parallel zueinander verlaufende Seiten = Grundseiten. Die beiden anderen Seiten bezeichnet man als Schenkel
2. es gibt je zwei benachbarte Winkel welche 180° ergeben (Supplementwinkel)

(die Höhe h ist der Abstand zwischen den beiden parallel verlaufenden Seiten)

Flächeninhalt: A = (a + c ) : 2 · h

Umfang: U = a + b + c + d

weitere Formeln: Formel Trapez

gleichschenkliges Trapez:

wie Trapez und zusätzlich:
1. die Schenkel sind gleich lang
2. ein gleichschenkliges Trapez kann auch ein Parallelogramm sein
3. neben den beiden Supplementwinkeln welche 180° ergeben sind die anderen beiden benachbarten Winkel gleich groß (symmetrisches Trapez) oder ergeben 180° (Parallelogramm)
4. im symmetrischen Trapez sind die Diagonalen gleich lang

(die Höhe h ist der Abstand zwischen den beiden parallel verlaufenden Seiten)

Flächeninhalt: A = (a + c ) : 2 · h

Umfang: U = a + b + c + b

weitere Formeln: Formel gleichschenkliges Trapez

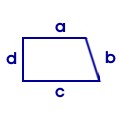
rechtwinkliges Trapez:

wie Trapez und zusätzlich:
1. mindestens zwei nebeneinander liegende rechte Winkel

Flächeninhalt: A = (a + c ) : 2 · d

Umfang: U = a + b + c + d

weitere Formeln: Formel rechtwinkliges Trapez

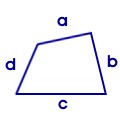
konvexes Viereck:

Vorgaben wie vier Seiten und ein Innenwinkel sind mehrdeutig! Die dem vorgegebenen Winkel gegenüberliegende Ecke kann dann konvex oder konkav sein! Hat man mehrere Winkel und Seitenlängen rechnet man den Flächeninhalt am besten über die durch einzeichnen der Diagonalen sich ergebenen Dreiecke.

weitere Formeln: Formel konvexes Viereck

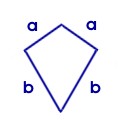
Drachenviereck (Deltoid):

1. ist symmetrisch zu einer Diagonalen
2. Diagonalen stehen senkrecht aufeinander
3. ein Paar gegenüberliegende Winkel sind gleich groß
4. zwei Paare gleich lange benachbarte Seiten

(e und f sind die Diagonalen)

Flächeninhalt: A = e · f : 2

Umfang: U = 2 · a + 2 · b
oder U = 2 · (a + b)

weitere Formeln: Formel Drachenviereck

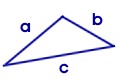
allgemeines Dreieck:

1. Summe der Innenwinkel = 180°
2. a + b > c

(h_c - ist die größte Höhe im Winkel von 90° über c)
Umfang: U = a + b + c

Flächeninhalt: (U = a + b + c)
A = √0,5U(0,5U-a)(0,5U-b)(0,5U-c)
oder
(β - Winkel zwischen a und b)
A = 0,5 · a · b · sin β
oder
A = c · h_c : 2
A = 0,5 · h_c · c

weitere Formeln: Formel allgemeines Dreieck

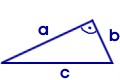
rechtwinkliges Dreieck:

wie allgemeines Dreieck und zusätzlich:
1. ein rechter Winkel 90°
2. die beiden andere Winkel zusammen 90°
3. a² + b² = c²

Flächeninhalt: A = 0,5 · a · b
oder
A = a · b : 2

Umfang: U = a + b + c

weitere Formeln: Formel rechtwinkliges Dreieck

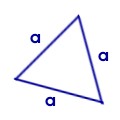
gleichseitiges Dreieck:

1. alle drei Seiten sind gleich lang
2. alle 3 Innenwinkel haben jeweils 60°

(h_a - ist die größte Höhe im Winkel von 90° über a)

Flächeninhalt: A = a² : 4 · √3
oder
A = a · h_a : 2
A = 0,5 · h_a · a

Umfang: U = 3 · a

weitere Formeln: Formel gleichseitiges Dreieck

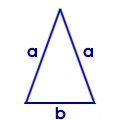
gleichschenkliges Dreieck:

a = Schenkel | b = Basis
1. mindestens zwei Seiten sind gleich lang
2. zwei Winkel gleich groß

(h_b - ist die größte Höhe im Winkel von 90° über b)

Flächeninhalt:
A = 0,5 · b · √a² - b² : 4
oder
A = b · h_b : 2
A = 0,5 · h_b · b

Umfang: U = 2 · a + b

weitere Formeln: Formel gleichschenkliges Dreieck

Kreis:

(d = Durchmesser | r = Radius |
pi=3.141592...)

Flächeninhalt: A = pi · r²
oder A = pi · d² : 4

Umfang: U = pi · 2 · r
oder U = pi · d

d = 2 · r
r = d : 2

weitere Formeln: Formel Kreis

Ellipse:

(a und b sind die Halbachsen)

Flächeninhalt: A = pi · a · b

weitere Formeln: Formel Ellipse

regelmäßiges Sechseck:

1. alle Seiten gleich lang
2. alle Innenwinkel =120°

Flächeninhalt: A = 3 : 2 · a² · √3

Umfang: U = 6 · a

weitere Formeln: Formel regelmäßiges Sechse

Flächeninhalt

MatheFormeln17

Status

Neuigkeiten